Leņķa definīcija ir "Leņķis ir plaknes daļa, ko ierobežo divi stari, kam ir kopīgs sākumpunkts". Bet angliski pieejamajās Montesori prezentācijās par leņķiem, kas paredzētas bērniem no 6 līdz 9 gadiem, netiek runāts par stariem un plaknēm. Par leņķi tiek runāts kā par laukumu starp diviem nogriežņiem, ko vizualizē, izmantojot ģeometrijas komplekta kociņus.
Es tomēr izvēlējos deviņgadnieku iepazīstināt ar leņķa definīciju un tāpēc atkārtojām vairākus ģeometrijas jēdzienus. Taisni un staru lieliski var nodemonstrēt ar diegu, lai rastos priekštats par to "bezgalīgumu". Roberts turēja diegu sākumpunktā, bet es to stiepu garumā, parādot, ka stars nekur nebeidzas. Mazliet atbrīvojot un tad atkal nospriegojot diegu, parādīju atšķirību starp līniju (kas var būt arī kā nenospriegots diegs) un taisni / staru (kas ir kā nospriegots diegs).
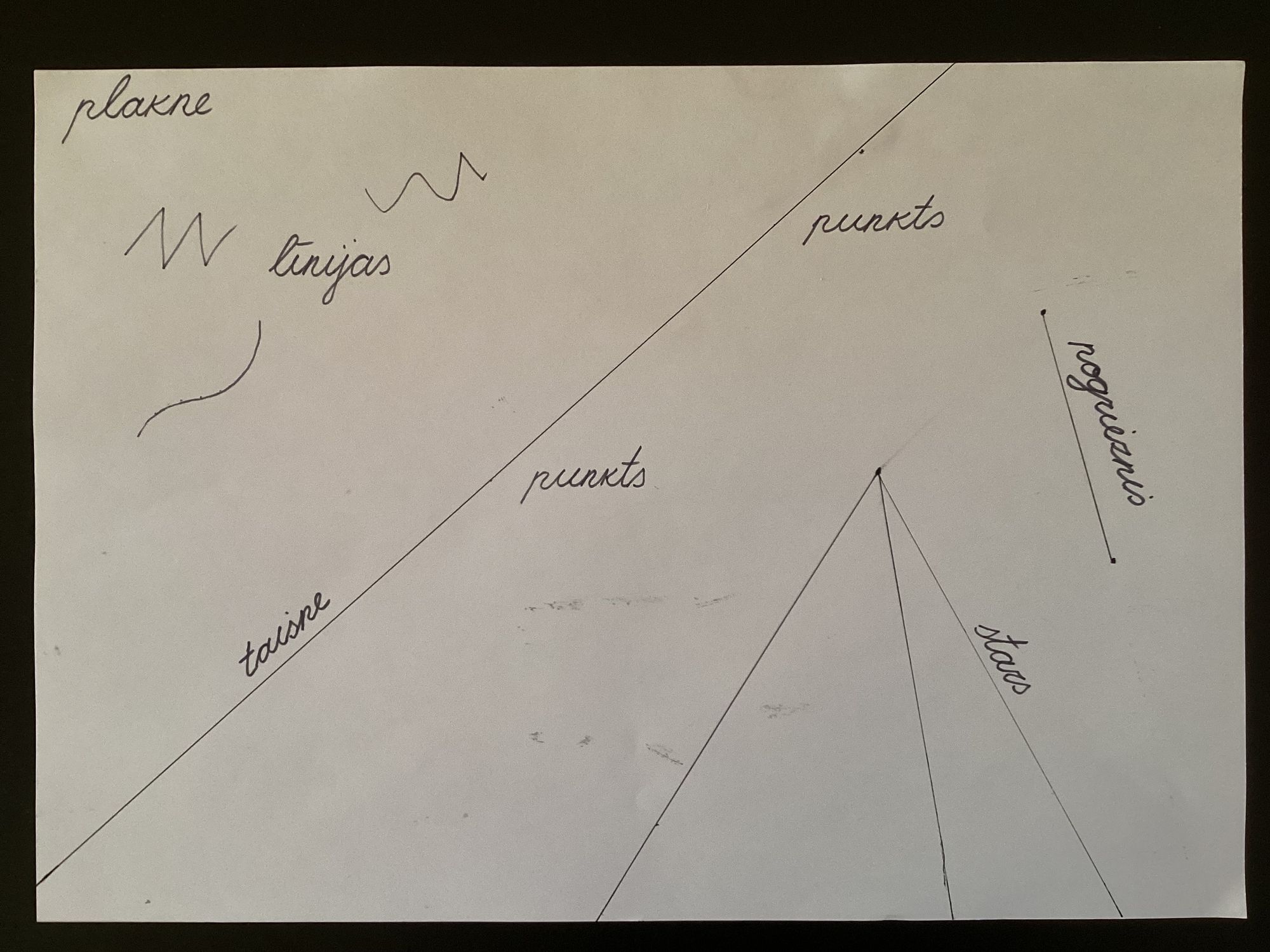
Tad es pārgāju uz leņķu demonstrēšanu, izmantojot kociņus, kas reprezentē nogriežņus - ar sākumu un beigām, bet ik pa laikam atgādināju, ka leņķis nebeidzas tur, kur beidzas kociņi.
Iepazīstināju ar leņķa elementiem.
Tad, pamazām attālinot kociņus, nodemonstrēju, ka leņķis var būt dažāda lieluma - no pavisam maziņa pat neredzama līdz pilnam aplim. No vairākiem kociņu komplektiem izveidoju leņķus, parādot, kādi ir leņķu veidi.
Pēc prezentācijas visu novācu, iedevu Robertam leņķu nosaukumus un aicināju tos sakārtot pēc lieluma, sākot ar mazāko. Tad aicināju pašam izveidot katra veida leņķi.
Lai tuvinātu leņķa jēdzienu dzīvei, pārrunājām, kāda veida leņķis veidojas starp pulksteņa rādītājiem, kad ir pulkstens 1.00, 2.00 u.t.t.
Nākamajā dienā stāstīju stāstu par to, kā radās doma leņķus mērīt grādos un, kāpēc pilns leņķis un pilns aplis ir 360 grādi. Stāstu biju īsumā pastāstījusi jau iepriekšējā dienā, braucot mašīnā, bet nu ķēros klāt stāstam ar vizuāliem atbalsta materiāliem - globusu, attēliem ar Babiloniju, zvaigznēm, zvaigžņu rotāciju, skaitļa 360 dalāmību.
Gatavojoties šim stāstam, pastaigas laikā pārrunāju, ko nozīmē kaut ko mērīt - jāizvēlas mērvienība un jānosaka mērvienību daudzums mērāmajā objektā. Mērvienība var būt gan sprīdis, gan pēda, gan akmens sviediens, bet daudzumu mēs parasti izsakām kā skaitli decimālajā sistēmā.
No angļu valodā pieejamajiem man vislabāk patika šī stāsta par 360 grādiem versija: https://www.youtube.com/watch?v=2PRsOn0t3Vw&list=PLQXOiMIrYFOdiFKabOcMwJtR1nsScDNFw&index=4
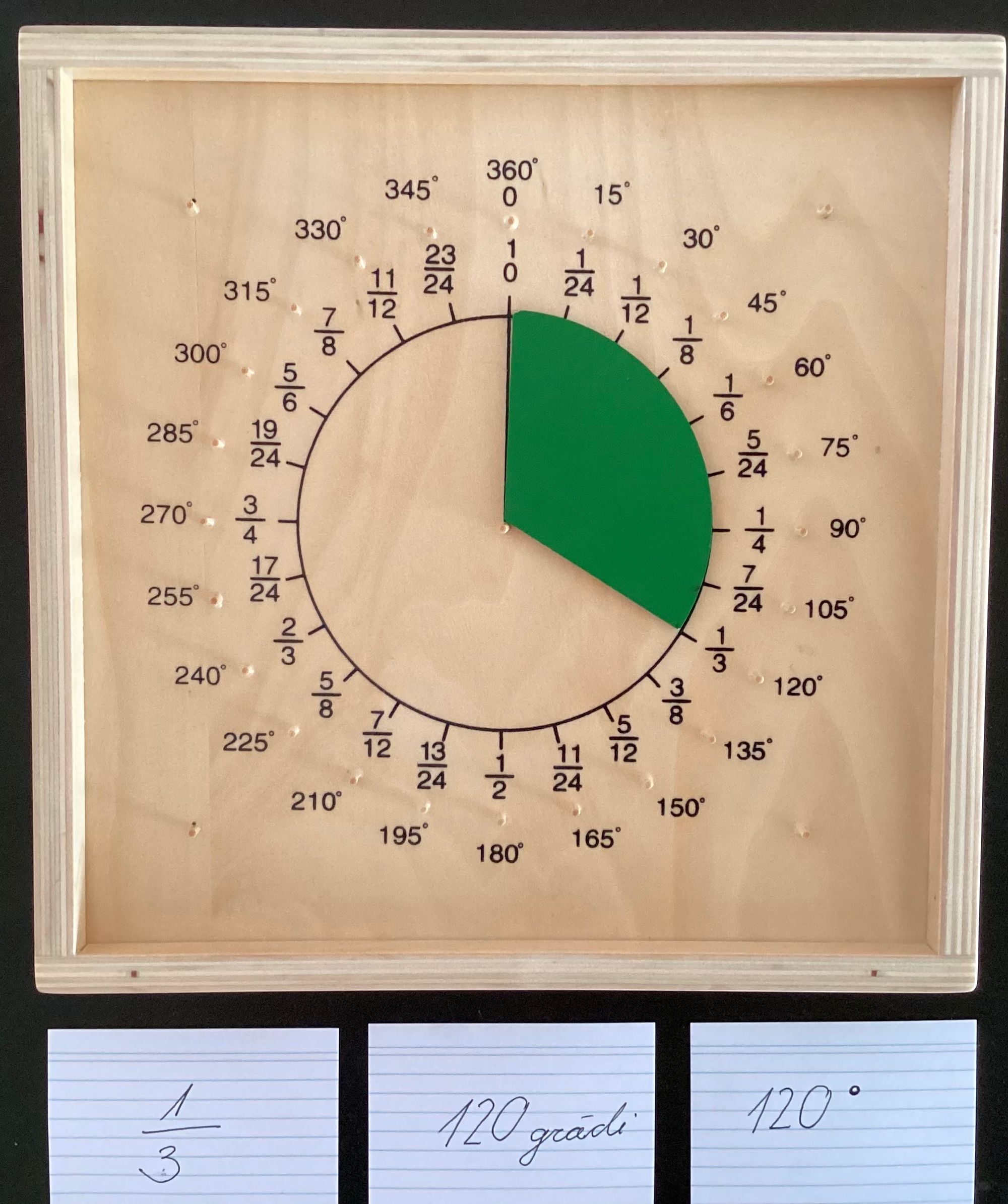
Kad ir skaidrs, kāpēc leņķus mēra grādos un kāpēc ir 360 grādi, Roberts ķeras klāt mērījumiem. Sākumā aicinu novērtēt, cik liels varētu būt leņķis kādai no daļām, un tad to izmērīt.
Pārrunājam to, ka daļu var izteikt grādos, un grādus apzīmē ar mazu aplīti pie skaitļa. Aicinu padomāt, kādus vēl vārdus matemātiķi ir saīsinājuši, lai būtu mazāk jāraksta - mm, kg, m u.t.t.
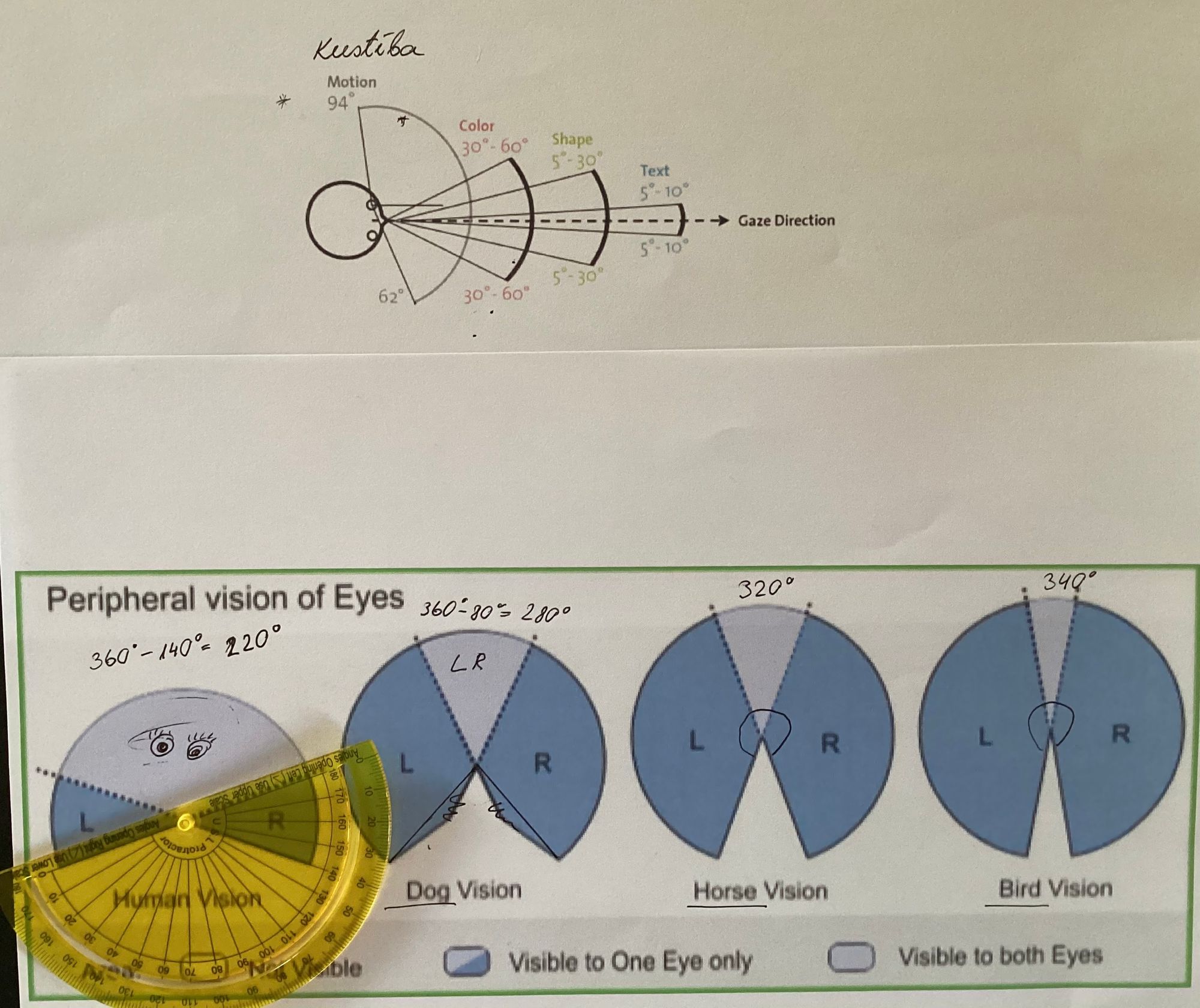
Nakamais solis - leņķu pielietojums. Kopīgi pētam, kā leņķos izsaka cilvēka un dzīvnieku redzes plašumu.
Mēram manu un Roberta špagatus, pirms tam tos nofotografējot.
Aicinu Robertu pavērot, kādus leņķus var atrast istabā. Secina, ka lielākā daļa ir taisni leņķi. Mēģina uzminēt un tad izmēra slīpā loga leņķi.
Citā dienā atkal atgriežamies pie leņķiem. Kurš no šiem leņķiem ir lielāks?
Kā leņķi sadalīt uz pusēm? Pirms tam gan jāiesildās un jāpamēģina ar cirkuļa un lineāla palīdzību uzvilkt nogrieznim perpendikulāru nogriezni, nogrieznim perpendikulāru nogriezni tieši caur atzīmētu punktu, sadalīt nogriezni uz pusēm. Tad var mēģināt sadalīt leņķi uz pusēm ar cirkuļa un lineāla vai tikai lineāla palīdzību un rezultātu pārbaudīt ar transportieri. Vieglāk izrādās ir darboties ar cirkuli nekā sadalīt uz pusēm 9 cm un 7 mm :)
Skat, cik dažādus leņķus veido koku stumbri un zari! Lai vieglāk tos saskatīt, var pārzīmēt uz cepampapīra. Kuram kokam zari ar stumbru veido šauru leņķi, visšaurāko leņķi, taisnu leņķi, platu leņķi?
Kādā leņķī jānovieto kārtis, lai tās neapgāztos? Interesanti, kāpēc? Kas mainās, mainot leņķi?
Kad apnīk "ķert" pareizo leņķi, var iemēģināt citu tehniku un papētīt, kādi te leņķi: https://www.youtube.com/watch?v=5F6j4e1C4Zk
Jautrs veids kā iepazīt leņķus. Metam kauliņus, zīmējam leņķus. Kurš pirmais iezīmēs pilnu apli? Cik trūkst līdz pilnam aplim? Par cik grādiem esam kļūdījušies, atzīmējot leņķus?
